Análisis predictivo con inteligencia artificial
López Oscar Leonardo
Índice
- Caso práctico de IA
- CIFAR10 Dataset
- Experimentos con redes neuronales densas
- Experimentos con CNNs
- Experimento Opcional
- Conclusión
In [3]:
#Importando TensorFlow import tensorflow as tf import numpy as np # Importando MatplotLib para mostrar gráficas de evaluación del modelo import matplotlib.pyplot as plt %matplotlib inline # Solucionamos una falla de Anaconda import os os.environ['KMP_DUPLICATE_LIB_OK']='True'
Caso práctico de IA
El objetivo de este caso práctico es demostrar cómo resolvería un análisis completo con Deep Learning, en el rol de data scientist dedicado a analizar y crear modelos de Deep Learning para pasarlos a producción y ser desplegados en una aplicación.
Imaginemos que tenemos un dataset completo que queremos explotar, y mi misión fuera utilizar este dataset de imágenes (CIFAR10) y realizar varios experimentos con distintas redes para descubrir cuál funciona mejor y cuál elegiría para pasar a producción. Por lo que además de tener que entrerar distintas redes y entender qué ha pasado en cada entrenamiento explicando el resultado, al final también justificaré cuál de todos los modelos entrenados es el más óptimo para pasar a producción.
Cada experimento a realizar está ya bien definido, a los fines de compartir este trabajo solamente tengo que crear la red neuronal con TensorFlow y realizar el entrenamiento de la misma. Por cada experimento les comento mis conclusiones de cómo de bueno o malo ha sido ese entrenamiento. Al final de todos los experimentos, termino con una pequeña documentación donde justifico cuál de los modelos entrenados es el más óptimo para pasar a producción.
Parte principal
La realización de cada uno de los experimentos definidos.
Destaco que el objetivo de este caso práctico no es obtener unos resultados muy buenos, de echo los resultados obtenidos son los pre-definidos por las redes que designo. El objetivo principal es mostrar desde mi paradigma profesional cómo abordaría un problema para ser resuelto con Deep Learning, partiendo de un dataset y un objetivo, y realizando diferentes experimentos hasta encontrar la solución más óptima a la que pueda llegar a desplegar en producción.
Parte adicional
La parte opcional se trata de proponer una propia red neuronal para obtener mejores resultados que los de la parte anterior. Obviamente… ¡Esta parte puedes verla como un reto!
Objetivos
- Cargar y explorar los datos del dataset CIFAR10 con los que se trabajarán.
- Crear cada una de las redes indicadas en los experimentos.
- Entrenar cada una de las redes creadas en los experimentos.
- Conclusiones del resultado de cada entrenamiento.
- Conclusión al final del cuaderno justificando el modelo elegido para desplegar.
CIFAR10 dataset
El dataset de de imágenes CIFAR10 tiene las siguintes características:
- Imágenes de 10 tipos de objetos: aviones, automóbiles, pájaros, gatos, ciervos, perros, ranas, caballos, barcos y camiones.
- Imágenes en color, es decir, cada pixel tiene 3 valores entre 0 y 255, esos valores corresponden a los valores de RGB (Red, Green, Blue).
- Imágenes de tamaño 32x32x3, 32×32 píxeles y 3 valores por pixel.
- 50.000 imágenes para el entrenamiento y 10.000 imágenes para el test.
Para empezar debemos descargar los datos de las bases de datos de Tensorflow.
In [13]:
cifar10 = tf.keras.datasets.cifar10 #Cargo el dataset en la variable (x_train, y_train), (x_test, y_test) = cifar10.load_data() #Cargo los datos labels = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'] #Etiquetado
Normalizamos los valores entre 0 y 1, para hacer el uso de la red mucho más eficiente ya que entre otra ventajas prácticas, la estimación mejora con entradas estandarizadas acotadas en un rango y también nos da la ventaja de simplificar los cambios de escala para los ajustes de pesos y sesgos.
In [14]:
x_train = x_train / 255.0 x_test = x_test / 255.0
In [15]:
# Muestro las imágenes
def show_images(images):
fig=plt.figure(figsize=(10, 10))
index = np.random.randint(len(images), size=100)
for i in range(100):
fig.add_subplot(10, 10, i+1)
plt.axis('off')
color = None
plt.imshow(images[index[i]].reshape([32, 32, 3]), cmap=color)
plt.show()
In [16]:
show_images(x_train)

Vemos que las imágenes son pequeñas, a color y pixeladas. Veamos a continuación más detalles:
In [18]:
print("Cantidad de imágenes para training: ", x_train.shape[0])
print("Cantidad de imágenes para test: ", x_test.shape[0])
print("Dimension de entrada: ", x_train.shape)
print("Dimension de salida: ", y_train.shape)
print("Indice de lista de salida: ", y_train[1])
print("Etiqueta correspondiente: ", labels[y_train[1][0]])
Cantidad de imágenes para training: 50000 Cantidad de imágenes para test: 10000 Dimension de entrada: (50000, 32, 32, 3) Dimension de salida: (50000, 1) Indice de lista de salida: [9] Etiqueta correspondiente: truck
Experimentos con redes neuronales densas
A continuación, realizo 2 experimentos usando redes neuronales densas
Experimento 1
Arquitectura de la red:
- Capa de aplanado
Flattencon entrada(32,32,3) - Capa densa
Densecon 10 neuronas y función de activación ReLU - Capa de salida densa
Densecon 10 neuronas y función de activación Softmax
Configuración del entrenamiento:
- Optimizador: Adam con factor de entrenamiento 0.01
- Función de error:
sparce_categorical_crossentropy - Métricas:
accuracy - Número de epochs: 20
Crear y entrenar la red neuronal indicada arriba
In [19]:
# Creación del modelo indicado model = tf.keras.models.Sequential([ #Objeto secuencial para procesar lista de capas tf.keras.layers.Flatten(input_shape=(32, 32,3)), #Aplanado de imagen tf.keras.layers.Dense(10, activation='relu'), #Capa Dense de 10 neuronas y función de activación ReLu tf.keras.layers.Dense(10, activation='softmax') #Capa de salida de 10 neuronas y función de activación Softmax ])
In [20]:
model.summary() #Resumen de la red neuronal
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= flatten (Flatten) (None, 3072) 0 _________________________________________________________________ dense (Dense) (None, 10) 30730 _________________________________________________________________ dense_1 (Dense) (None, 10) 110 ================================================================= Total params: 30,840 Trainable params: 30,840 Non-trainable params: 0 _________________________________________________________________
In [ ]:
En sólo estas dos capas ya calcula 30.840 parámetros !
In [21]:
# Entrenamiento:
# Definimos el optimizador cambiando el factor de entrenamiento
opt = tf.keras.optimizers.Adam(learning_rate=0.01) #Optimizador Adam, con cambio de pesos de a 0,01
# Compilamos el modelo
model.compile(optimizer=opt,
loss='sparse_categorical_crossentropy', #La función de error es categórica, ya que estamos clasificando
metrics=['accuracy']) #La métrica buscada es la precisión, por ser clasificación
In [23]:
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=20) # 20 veces vamos a entrenar nuestra red
Epoch 1/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3039 - accuracy: 0.0994 - val_loss: 2.3059 - val_accuracy: 0.1000 Epoch 2/20 1563/1563 [==============================] - 4s 2ms/step - loss: 2.3039 - accuracy: 0.0993 - val_loss: 2.3042 - val_accuracy: 0.1000 Epoch 3/20 1563/1563 [==============================] - 4s 2ms/step - loss: 2.3041 - accuracy: 0.0958 - val_loss: 2.3042 - val_accuracy: 0.1000 Epoch 4/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3040 - accuracy: 0.0988 - val_loss: 2.3034 - val_accuracy: 0.1000 Epoch 5/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3040 - accuracy: 0.1007 - val_loss: 2.3030 - val_accuracy: 0.1000 Epoch 6/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3040 - accuracy: 0.0994 - val_loss: 2.3028 - val_accuracy: 0.1000 Epoch 7/20 1563/1563 [==============================] - 4s 2ms/step - loss: 2.3040 - accuracy: 0.1000 - val_loss: 2.3035 - val_accuracy: 0.1000 Epoch 8/20 1563/1563 [==============================] - 4s 2ms/step - loss: 2.3041 - accuracy: 0.0996 - val_loss: 2.3030 - val_accuracy: 0.1000 Epoch 9/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3041 - accuracy: 0.0995 - val_loss: 2.3036 - val_accuracy: 0.1000 Epoch 10/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3039 - accuracy: 0.1012 - val_loss: 2.3046 - val_accuracy: 0.1000 Epoch 11/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3041 - accuracy: 0.0981 - val_loss: 2.3047 - val_accuracy: 0.1000 Epoch 12/20 1563/1563 [==============================] - 4s 2ms/step - loss: 2.3040 - accuracy: 0.0983 - val_loss: 2.3035 - val_accuracy: 0.1000 Epoch 13/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3041 - accuracy: 0.0969 - val_loss: 2.3041 - val_accuracy: 0.1000 Epoch 14/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3041 - accuracy: 0.0996 - val_loss: 2.3039 - val_accuracy: 0.1000 Epoch 15/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3040 - accuracy: 0.1010 - val_loss: 2.3033 - val_accuracy: 0.1000 Epoch 16/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3041 - accuracy: 0.0995 - val_loss: 2.3034 - val_accuracy: 0.1000 Epoch 17/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3039 - accuracy: 0.1001 - val_loss: 2.3036 - val_accuracy: 0.1000 Epoch 18/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3039 - accuracy: 0.1041 - val_loss: 2.3037 - val_accuracy: 0.1000 Epoch 19/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3040 - accuracy: 0.0982 - val_loss: 2.3038 - val_accuracy: 0.1000 Epoch 20/20 1563/1563 [==============================] - 3s 2ms/step - loss: 2.3039 - accuracy: 0.0987 - val_loss: 2.3040 - val_accuracy: 0.1000
Resultado obtenidos
La precisión no ha ido aumentando con cada epoch sino que ha sido variable y baja. Por otro lado el error y la validación se han mantenido practicamente constante, lo que nos indica que la red tampoco ha aprendido. Todo esto era de esperararse ante una red demasiado simple, ya son muy pocas capas, neuronas y epochs para imágenes de colores.
Experimento 2
Arquitectura de la red:
- Capa de aplanado
Flattencon entrada(32,32,3). - Capa densa
Densecon 32 neuronas y función de activación ReLU. - Capa densa
Densecon 64 neuronas y función de activación ReLU. - Capa densa
Densecon 128 neuronas y función de activación ReLU. - Capa de salida densa
Densecon 10 neuronas y función de activación Softmax.
Configuración del entrenamiento:
- Optimizador: Adam con factor de entrenamiento 0.001
- Función de error:
sparce_categorical_crossentropy. - Métricas:
accuracy. - Número de epochs: 40
Crear y entrenar la red neuronal indicada arriba
In [24]:
# Creación del modelo indicado model = tf.keras.models.Sequential([ #Objeto secuencial para procesar lista de capas tf.keras.layers.Flatten(input_shape=(32, 32,3)), #Aplanado de imagen tf.keras.layers.Dense(32, activation='relu'), #Capa Dense de 32 neuronas y función de activación ReLu tf.keras.layers.Dense(64, activation='relu'), #Capa Dense de 64 neuronas y función de activación ReLu tf.keras.layers.Dense(128, activation='relu'), #Capa Dense de 128 neuronas y función de activación ReLu tf.keras.layers.Dense(10, activation='softmax') #Capa de salida de 10 neuronas y función de activación Softmax ])
In [25]:
model.summary() #Resumen de la nueva red neuronal
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= flatten_1 (Flatten) (None, 3072) 0 _________________________________________________________________ dense_2 (Dense) (None, 32) 98336 _________________________________________________________________ dense_3 (Dense) (None, 64) 2112 _________________________________________________________________ dense_4 (Dense) (None, 128) 8320 _________________________________________________________________ dense_5 (Dense) (None, 10) 1290 ================================================================= Total params: 110,058 Trainable params: 110,058 Non-trainable params: 0 _________________________________________________________________
In [ ]:
Ahora ya tenemos 4 capas y ya calcula 110.058 parámetros !
In [26]:
# Entrenamiento:
# Definimos el optimizador cambiando el factor de entrenamiento
opt = tf.keras.optimizers.Adam(learning_rate=0.001) #Optimizador Adam, con menor cambio de pesos de a 0,001
# Compilamos el modelo
model.compile(optimizer=opt,
loss='sparse_categorical_crossentropy', #La función de error es categórica, ya que estamos clasificando
metrics=['accuracy']) #La métrica buscada es la precisión, por ser clasificación
In [27]:
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=40) # 40 veces vamos a entrenar nuestra red
Epoch 1/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.8880 - accuracy: 0.3056 - val_loss: 1.7703 - val_accuracy: 0.3570 Epoch 2/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.7259 - accuracy: 0.3756 - val_loss: 1.7895 - val_accuracy: 0.3575 Epoch 3/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.6772 - accuracy: 0.3938 - val_loss: 1.6598 - val_accuracy: 0.3996 Epoch 4/40 1563/1563 [==============================] - 4s 3ms/step - loss: 1.6476 - accuracy: 0.4023 - val_loss: 1.6328 - val_accuracy: 0.4169 Epoch 5/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.6270 - accuracy: 0.4123 - val_loss: 1.6085 - val_accuracy: 0.4256 Epoch 6/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.6102 - accuracy: 0.4168 - val_loss: 1.6199 - val_accuracy: 0.4219 Epoch 7/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5968 - accuracy: 0.4248 - val_loss: 1.5964 - val_accuracy: 0.4303 Epoch 8/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5875 - accuracy: 0.4264 - val_loss: 1.6376 - val_accuracy: 0.4144 Epoch 9/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5766 - accuracy: 0.4314 - val_loss: 1.6150 - val_accuracy: 0.4207 Epoch 10/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5658 - accuracy: 0.4338 - val_loss: 1.6034 - val_accuracy: 0.4276 Epoch 11/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5568 - accuracy: 0.4386 - val_loss: 1.5886 - val_accuracy: 0.4307 Epoch 12/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5482 - accuracy: 0.4436 - val_loss: 1.5786 - val_accuracy: 0.4321 Epoch 13/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5433 - accuracy: 0.4419 - val_loss: 1.5761 - val_accuracy: 0.4377 Epoch 14/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5377 - accuracy: 0.4452 - val_loss: 1.5803 - val_accuracy: 0.4389 Epoch 15/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5303 - accuracy: 0.4487 - val_loss: 1.5791 - val_accuracy: 0.4397 Epoch 16/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.5250 - accuracy: 0.4498 - val_loss: 1.5555 - val_accuracy: 0.4446 Epoch 17/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5243 - accuracy: 0.4498 - val_loss: 1.5676 - val_accuracy: 0.4382 Epoch 18/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5135 - accuracy: 0.4552 - val_loss: 1.5758 - val_accuracy: 0.4386 Epoch 19/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5099 - accuracy: 0.4534 - val_loss: 1.6062 - val_accuracy: 0.4386 Epoch 20/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5069 - accuracy: 0.4546 - val_loss: 1.5549 - val_accuracy: 0.4464 Epoch 21/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.5025 - accuracy: 0.4564 - val_loss: 1.5956 - val_accuracy: 0.4319 Epoch 22/40 1563/1563 [==============================] - 4s 3ms/step - loss: 1.4975 - accuracy: 0.4595 - val_loss: 1.5743 - val_accuracy: 0.4406 Epoch 23/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4913 - accuracy: 0.4623 - val_loss: 1.5929 - val_accuracy: 0.4345 Epoch 24/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4888 - accuracy: 0.4635 - val_loss: 1.5918 - val_accuracy: 0.4344 Epoch 25/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4874 - accuracy: 0.4632 - val_loss: 1.5929 - val_accuracy: 0.4372 Epoch 26/40 1563/1563 [==============================] - 4s 3ms/step - loss: 1.4822 - accuracy: 0.4633 - val_loss: 1.5537 - val_accuracy: 0.4489 Epoch 27/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4782 - accuracy: 0.4651 - val_loss: 1.5625 - val_accuracy: 0.4417 Epoch 28/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4772 - accuracy: 0.4649 - val_loss: 1.5642 - val_accuracy: 0.4433 Epoch 29/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4697 - accuracy: 0.4659 - val_loss: 1.5791 - val_accuracy: 0.4412 Epoch 30/40 1563/1563 [==============================] - 4s 3ms/step - loss: 1.4679 - accuracy: 0.4708 - val_loss: 1.5722 - val_accuracy: 0.4401 Epoch 31/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4665 - accuracy: 0.4699 - val_loss: 1.5573 - val_accuracy: 0.4486 Epoch 32/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4638 - accuracy: 0.4700 - val_loss: 1.5780 - val_accuracy: 0.4368 Epoch 33/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4636 - accuracy: 0.4699 - val_loss: 1.6006 - val_accuracy: 0.4332 Epoch 34/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4572 - accuracy: 0.4748 - val_loss: 1.5586 - val_accuracy: 0.4515 Epoch 35/40 1563/1563 [==============================] - 4s 3ms/step - loss: 1.4556 - accuracy: 0.4743 - val_loss: 1.6132 - val_accuracy: 0.4280 Epoch 36/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4516 - accuracy: 0.4743 - val_loss: 1.5695 - val_accuracy: 0.4467 Epoch 37/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4512 - accuracy: 0.4748 - val_loss: 1.5817 - val_accuracy: 0.4413 Epoch 38/40 1563/1563 [==============================] - 3s 2ms/step - loss: 1.4496 - accuracy: 0.4768 - val_loss: 1.5612 - val_accuracy: 0.4483 Epoch 39/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4456 - accuracy: 0.4767 - val_loss: 1.5978 - val_accuracy: 0.4433 Epoch 40/40 1563/1563 [==============================] - 4s 2ms/step - loss: 1.4411 - accuracy: 0.4814 - val_loss: 1.5625 - val_accuracy: 0.4491
In [28]:
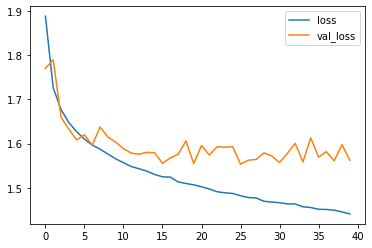
# Evaluando el modelo plt.plot(hist.history['loss'], label='loss') plt.plot(hist.history['val_loss'], label='val_loss') plt.legend()
Out[28]:
<matplotlib.legend.Legend at 0x26236e0ce80>
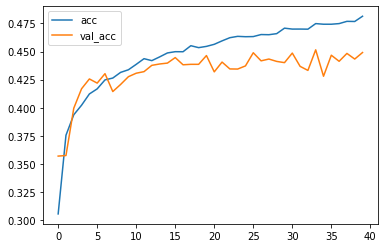
plt.plot(hist.history['accuracy'], label='acc') plt.plot(hist.history['val_accuracy'], label='val_acc') plt.legend()
Resultado obtenidos
Aquí el modelo ya tiene mucho más sentido al ver cómo mejora la precisión y se reduce el error al duplicar las capas con mas neuronas y aumentando también el número de epochs. Resulta por lo menos mejor que el primero para la clasificación de imágenes a color.
Experimentos con CNNs
A continuación, realizar 2 experimentos usando redes convolucionales con las redes que se te indican en cada sección.
Experimento 3
Arquitectura de la red:
- Capa convolucional
Conv2Dcon 16 filtros/kernels, padding con relleno, activación ReLU y con entrada(32,32,3) - Capa pooling
MaxPool2Dcon reducción de 2 tanto en tamaño como en desplazamiento (stride) y padding con relleno. - Capa de aplanado
Flatten. - Capa densa
Densecon 64 neuronas y función de activación ReLU. - Capa densa
Densecon 32 neuronas y función de activación ReLU. - Capa de salida densa
Densecon 10 neuronas y función de activación Softmax.
Configuración del entrenamiento:
- Optimizador: Adam con factor de entrenamiento 0.0001
- Función de error:
sparce_categorical_crossentropy. - Métricas:
accuracy. - Número de epochs: 10
Crear y entrenar la red neuronal indicada arriba
In [30]:
# Definimos la red convolucional
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16, (5, 5), padding="same", activation="relu", input_shape=(32,32,3)),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"), #Pooling de reducción a la mitad
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation="relu"), #Capa Dense de 64 neuronas y función de activación ReLu
tf.keras.layers.Dense(32, activation="relu"), #Capa Dense de 32 neuronas y función de activación ReLu
tf.keras.layers.Dense(10, activation="softmax") #Capa Dense de salida 12 neuronas y función de activación Softmax
])
# definimos el optimizador
opt = tf.keras.optimizers.Adam(learning_rate=0.0001)
# compilamos el modelo
model.compile(optimizer=opt,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# visualizamos modelo
model.summary()
Model: "sequential_2" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 32, 32, 16) 1216 _________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 16, 16, 16) 0 _________________________________________________________________ flatten_2 (Flatten) (None, 4096) 0 _________________________________________________________________ dense_6 (Dense) (None, 64) 262208 _________________________________________________________________ dense_7 (Dense) (None, 32) 2080 _________________________________________________________________ dense_8 (Dense) (None, 10) 330 ================================================================= Total params: 265,834 Trainable params: 265,834 Non-trainable params: 0 _________________________________________________________________
In [31]:
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=10) # 10 veces vamos a entrenar nuestra red
Epoch 1/10 1563/1563 [==============================] - 42s 27ms/step - loss: 1.8228 - accuracy: 0.3511 - val_loss: 1.6597 - val_accuracy: 0.4191 Epoch 2/10 1563/1563 [==============================] - 44s 28ms/step - loss: 1.5487 - accuracy: 0.4476 - val_loss: 1.4826 - val_accuracy: 0.4674 Epoch 3/10 1563/1563 [==============================] - 43s 28ms/step - loss: 1.4363 - accuracy: 0.4878 - val_loss: 1.4226 - val_accuracy: 0.4837 Epoch 4/10 1563/1563 [==============================] - 41s 26ms/step - loss: 1.3621 - accuracy: 0.5135 - val_loss: 1.3457 - val_accuracy: 0.5260 Epoch 5/10 1563/1563 [==============================] - 41s 26ms/step - loss: 1.3075 - accuracy: 0.5349 - val_loss: 1.3080 - val_accuracy: 0.5321 Epoch 6/10 1563/1563 [==============================] - 42s 27ms/step - loss: 1.2665 - accuracy: 0.5507 - val_loss: 1.2746 - val_accuracy: 0.5425 Epoch 7/10 1563/1563 [==============================] - 41s 26ms/step - loss: 1.2321 - accuracy: 0.5646 - val_loss: 1.2452 - val_accuracy: 0.5594 Epoch 8/10 1563/1563 [==============================] - 38s 24ms/step - loss: 1.2024 - accuracy: 0.5750 - val_loss: 1.2437 - val_accuracy: 0.5569 Epoch 9/10 1563/1563 [==============================] - 39s 25ms/step - loss: 1.1741 - accuracy: 0.5847 - val_loss: 1.2263 - val_accuracy: 0.5623 Epoch 10/10 1563/1563 [==============================] - 39s 25ms/step - loss: 1.1498 - accuracy: 0.5957 - val_loss: 1.2235 - val_accuracy: 0.5661
Resultado obtenidos
La precisión ha ido mejorando aunque sólo hasta un 59%, y el error fué disminuyendo. En validación sólo del 56%.
In [32]:
# Gráficamente: fig=plt.figure(figsize=(60, 40)) # error fig.add_subplot(10, 10, 2) plt.plot(hist.history['loss'], label='loss') plt.plot(hist.history['val_loss'], label='val_loss') # precision fig.add_subplot(10, 10, 1) plt.plot(hist.history['accuracy'], label='acc') plt.plot(hist.history['val_accuracy'], label='val_acc') plt.legend() plt.legend() plt.show()
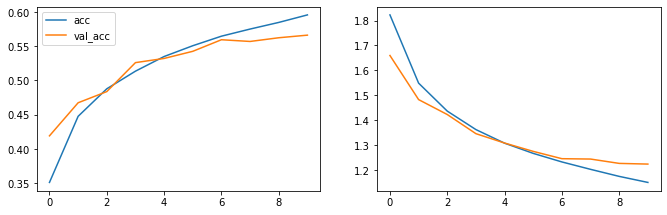
Experimento 4
Arquitectura de la red:
- Capa convolucional
Conv2Dcon 32 filtros/kernels, padding con relleno, activación ReLU y con entrada(32,32,3) - Capa pooling
MaxPool2Dcon reducción de 2 tanto en tamaño como en desplazamiento (stride) y padding con relleno. - Capa convolucional
Conv2Dcon 64 filtros/kernels, padding con relleno y activación ReLU - Capa pooling
MaxPool2Dcon reducción de 2 tanto en tamaño como en desplazamiento (stride) y padding con relleno. - Capa convolucional
Conv2Dcon 64 filtros/kernels, padding con relleno y activación ReLU - Capa pooling
MaxPool2Dcon reducción de 2 tanto en tamaño como en desplazamiento (stride) y padding con relleno. - Capa de aplanado
Flatten. - Capa densa
Densecon 64 neuronas y función de activación ReLU. - Capa de salida densa
Densecon 10 neuronas y función de activación Softmax.
Configuración del entrenamiento:
- Optimizador: Adam con factor de entrenamiento 0.001
- Función de error:
sparce_categorical_crossentropy. - Métricas:
accuracy. - Número de epochs: 20
COMPLETAR: crear y entrena la red neuronal indicada arriba
In [33]:
# Definimos la nueva mejorada red con 3 capas convolucionales
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3, 3), padding="same", activation="relu", input_shape=(32,32,3)),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"),
tf.keras.layers.Conv2D(64, (3, 3), padding="same", activation="relu"),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"),
tf.keras.layers.Conv2D(64, (3, 3), padding="same", activation="relu"),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")
])
# definimos el optimizador
opt = tf.keras.optimizers.Adam(learning_rate=0.001)
# compilamos el modelo
model.compile(optimizer=opt,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
Model: "sequential_3" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_1 (Conv2D) (None, 32, 32, 32) 896 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 16, 16, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 16, 16, 64) 18496 _________________________________________________________________ max_pooling2d_2 (MaxPooling2 (None, 8, 8, 64) 0 _________________________________________________________________ conv2d_3 (Conv2D) (None, 8, 8, 64) 36928 _________________________________________________________________ max_pooling2d_3 (MaxPooling2 (None, 4, 4, 64) 0 _________________________________________________________________ flatten_3 (Flatten) (None, 1024) 0 _________________________________________________________________ dense_9 (Dense) (None, 64) 65600 _________________________________________________________________ dense_10 (Dense) (None, 10) 650 ================================================================= Total params: 122,570 Trainable params: 122,570 Non-trainable params: 0 _________________________________________________________________
In [34]:
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=20)
Epoch 1/20 1563/1563 [==============================] - 92s 59ms/step - loss: 1.4393 - accuracy: 0.4801 - val_loss: 1.1341 - val_accuracy: 0.5960 Epoch 2/20 1563/1563 [==============================] - 96s 62ms/step - loss: 1.0293 - accuracy: 0.6372 - val_loss: 1.0027 - val_accuracy: 0.6555 Epoch 3/20 1563/1563 [==============================] - 98s 63ms/step - loss: 0.8829 - accuracy: 0.6912 - val_loss: 0.8941 - val_accuracy: 0.6931 Epoch 4/20 1563/1563 [==============================] - 87s 56ms/step - loss: 0.7844 - accuracy: 0.7255 - val_loss: 0.8965 - val_accuracy: 0.6940 Epoch 5/20 1563/1563 [==============================] - 84s 54ms/step - loss: 0.7143 - accuracy: 0.7511 - val_loss: 0.8104 - val_accuracy: 0.7233 Epoch 6/20 1563/1563 [==============================] - 85s 55ms/step - loss: 0.6531 - accuracy: 0.7722 - val_loss: 0.8476 - val_accuracy: 0.7138 Epoch 7/20 1563/1563 [==============================] - 86s 55ms/step - loss: 0.6069 - accuracy: 0.7875 - val_loss: 0.8130 - val_accuracy: 0.7284 Epoch 8/20 1563/1563 [==============================] - 84s 54ms/step - loss: 0.5673 - accuracy: 0.8015 - val_loss: 0.8330 - val_accuracy: 0.7210 Epoch 9/20 1563/1563 [==============================] - 87s 56ms/step - loss: 0.5283 - accuracy: 0.8120 - val_loss: 0.8181 - val_accuracy: 0.7346 Epoch 10/20 1563/1563 [==============================] - 84s 54ms/step - loss: 0.4838 - accuracy: 0.8285 - val_loss: 0.8473 - val_accuracy: 0.7314 Epoch 11/20 1563/1563 [==============================] - 84s 54ms/step - loss: 0.4552 - accuracy: 0.8404 - val_loss: 0.8573 - val_accuracy: 0.7273 Epoch 12/20 1563/1563 [==============================] - 85s 54ms/step - loss: 0.4229 - accuracy: 0.8490 - val_loss: 0.9197 - val_accuracy: 0.7265 Epoch 13/20 1563/1563 [==============================] - 87s 55ms/step - loss: 0.3993 - accuracy: 0.8578 - val_loss: 0.8927 - val_accuracy: 0.7350 Epoch 14/20 1563/1563 [==============================] - 85s 55ms/step - loss: 0.3724 - accuracy: 0.8678 - val_loss: 0.9579 - val_accuracy: 0.7244 Epoch 15/20 1563/1563 [==============================] - 86s 55ms/step - loss: 0.3457 - accuracy: 0.8750 - val_loss: 0.9808 - val_accuracy: 0.7232 Epoch 16/20 1563/1563 [==============================] - 87s 55ms/step - loss: 0.3232 - accuracy: 0.8842 - val_loss: 1.0162 - val_accuracy: 0.7296 Epoch 17/20 1563/1563 [==============================] - 86s 55ms/step - loss: 0.3034 - accuracy: 0.8889 - val_loss: 1.0350 - val_accuracy: 0.7302 Epoch 18/20 1563/1563 [==============================] - 90s 57ms/step - loss: 0.2859 - accuracy: 0.8963 - val_loss: 1.0985 - val_accuracy: 0.7278 Epoch 19/20 1563/1563 [==============================] - 85s 54ms/step - loss: 0.2661 - accuracy: 0.9044 - val_loss: 1.1589 - val_accuracy: 0.7232 Epoch 20/20 1563/1563 [==============================] - 84s 54ms/step - loss: 0.2517 - accuracy: 0.9084 - val_loss: 1.1741 - val_accuracy: 0.7195
In [35]:
# Gráficamente: fig=plt.figure(figsize=(60, 40)) # error fig.add_subplot(10, 10, 2) plt.plot(hist.history['loss'], label='loss') plt.plot(hist.history['val_loss'], label='val_loss') # precision fig.add_subplot(10, 10, 1) plt.plot(hist.history['accuracy'], label='acc') plt.plot(hist.history['val_accuracy'], label='val_acc') plt.legend() plt.legend() plt.show()
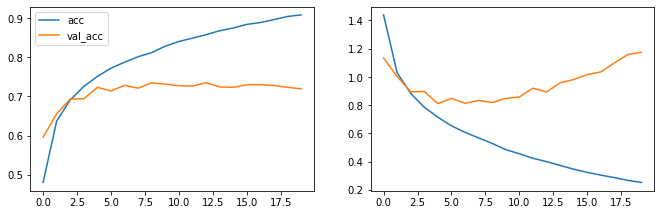
Resultado obtenidos
A priori los cálculos son muy prometedores ya que la precisión mejora y crece notablemente hasta un 90%, pero en la gráfica vemos la validación cómo se estanca rápidamente lo cual nos marca un notable sobreentrenamiento del modelo que para posibles nuevas imágenes fallaría demasiado.
Parte adicional
Esta parte de reto, se trata de realizar mi propia red neuronal para intentar mejorar lo aprendido en las anteriores redes o al menos acercarse a la red que mejor ha funcionado. El objetivo es proponer una posible red que pueda funcionar y se pueda poner en práctica para ver cómo funciona y comentarles los resultados logrados.
In [47]:
# Mi red propuesta
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3, 3), padding="same", activation="relu", input_shape=(32,32,3)),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"),
tf.keras.layers.Dropout(0.2), #Para evitar el sobreentrenamiento
tf.keras.layers.Conv2D(64, (3, 3), padding="same", activation="relu"),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"),
tf.keras.layers.Dropout(0.2), #Para evitar el sobreentrenamiento
tf.keras.layers.Conv2D(64, (3, 3), padding="same", activation="relu"),
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=(2, 2), padding="same"),
tf.keras.layers.Dropout(0.2), #Para evitar el sobreentrenamiento
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation="relu"),
tf.keras.layers.Dense(64, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")
])
# definimos el optimizador
opt = tf.keras.optimizers.Adam(learning_rate=0.001)
# compilamos el modelo
model.compile(optimizer=opt,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
Model: "sequential_10" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_22 (Conv2D) (None, 32, 32, 32) 896 _________________________________________________________________ max_pooling2d_22 (MaxPooling (None, 16, 16, 32) 0 _________________________________________________________________ dropout_18 (Dropout) (None, 16, 16, 32) 0 _________________________________________________________________ conv2d_23 (Conv2D) (None, 16, 16, 64) 18496 _________________________________________________________________ max_pooling2d_23 (MaxPooling (None, 8, 8, 64) 0 _________________________________________________________________ dropout_19 (Dropout) (None, 8, 8, 64) 0 _________________________________________________________________ conv2d_24 (Conv2D) (None, 8, 8, 64) 36928 _________________________________________________________________ max_pooling2d_24 (MaxPooling (None, 4, 4, 64) 0 _________________________________________________________________ dropout_20 (Dropout) (None, 4, 4, 64) 0 _________________________________________________________________ flatten_8 (Flatten) (None, 1024) 0 _________________________________________________________________ dense_31 (Dense) (None, 128) 131200 _________________________________________________________________ dense_32 (Dense) (None, 64) 8256 _________________________________________________________________ dense_33 (Dense) (None, 10) 650 ================================================================= Total params: 196,426 Trainable params: 196,426 Non-trainable params: 0 _________________________________________________________________
In [48]:
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=10)
Epoch 1/10 1563/1563 [==============================] - 96s 61ms/step - loss: 1.5697 - accuracy: 0.4245 - val_loss: 1.2786 - val_accuracy: 0.5457 Epoch 2/10 1563/1563 [==============================] - 94s 60ms/step - loss: 1.1720 - accuracy: 0.5781 - val_loss: 0.9948 - val_accuracy: 0.6490 Epoch 3/10 1563/1563 [==============================] - 93s 60ms/step - loss: 1.0163 - accuracy: 0.6389 - val_loss: 0.9087 - val_accuracy: 0.6758 Epoch 4/10 1563/1563 [==============================] - 98s 63ms/step - loss: 0.9299 - accuracy: 0.6710 - val_loss: 0.8778 - val_accuracy: 0.6937 Epoch 5/10 1563/1563 [==============================] - 93s 60ms/step - loss: 0.8656 - accuracy: 0.6954 - val_loss: 0.8424 - val_accuracy: 0.7070 Epoch 6/10 1563/1563 [==============================] - 93s 60ms/step - loss: 0.8179 - accuracy: 0.7129 - val_loss: 0.7994 - val_accuracy: 0.7223 Epoch 7/10 1563/1563 [==============================] - 98s 63ms/step - loss: 0.7805 - accuracy: 0.7258 - val_loss: 0.7911 - val_accuracy: 0.7230 Epoch 8/10 1563/1563 [==============================] - 101s 65ms/step - loss: 0.7479 - accuracy: 0.7369 - val_loss: 0.7612 - val_accuracy: 0.7341 Epoch 9/10 1563/1563 [==============================] - 101s 65ms/step - loss: 0.7199 - accuracy: 0.7461 - val_loss: 0.7642 - val_accuracy: 0.7362 Epoch 10/10 1563/1563 [==============================] - 100s 64ms/step - loss: 0.7031 - accuracy: 0.7509 - val_loss: 0.7145 - val_accuracy: 0.7557
In [49]:
# Gráficamente: fig=plt.figure(figsize=(60, 40)) # error fig.add_subplot(10, 10, 2) plt.plot(hist.history['loss'], label='loss') plt.plot(hist.history['val_loss'], label='val_loss') # precision fig.add_subplot(10, 10, 1) plt.plot(hist.history['accuracy'], label='acc') plt.plot(hist.history['val_accuracy'], label='val_acc') plt.legend() plt.legend() plt.show()
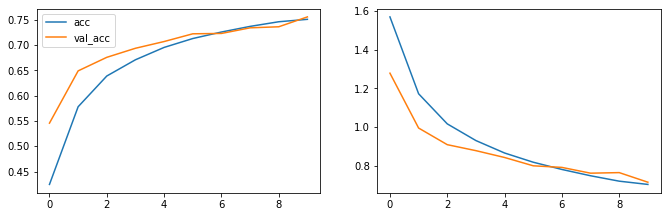
Resultado obtenidos
Aquí logré obtener por un lado una buena precisión del 75% y las gráficas de curvas muy similares con un muy buen control del sobreajuste con la función Dropout, donde fui probando diferentes porcentajes.
Conclusión final
Luego de crear los modelos de redes indicados y experimentar diferentes entrenamientos en la parte opcional, concluyo que claramente las redes convolucionales tienen un mejor ajuste respecto a las neuronales para la clasificación de imágenes a color. Este proyecto es de introduccción para el Deep Learning con TensorFlow, pues realmente desarrollar experiencia con mucha práctica es la clave para lograr la habilidad de identificar los ajustes óptimos de capas, filtros, funciones, neuronas, etc. que nos permitirán lograr entrenamientos de alta performance.
Muchas gracias !
