Segmentación de clientes
Ing. Lopez Leonardo
Proyecto:
Se deberán realizar los siguientes análisis:
1)Análisis descriptivo, ¿qué datos tenemos?
2)Segmentación de los clientes con la recencia y la frecuencia.
3)Segmentación de los clientes con el gasto total y la frecuencia de compra.
4)Análisis de agrupaciones, realizar:
Dendograma de la tipología de productos por el total gasto de cada cliente (cantidad por precio).1) Análisis descriptivo
En el análisis de analítica clásica comenzamos con una exploración general de los datos para observar qué tipos de datos manejaremos
#Primero leemos el fichero cData del directorio C
cData<-read.table("/cloud/project/Clustering/TransactionsCasoPractico.csv", header=TRUE, sep = ";")
head(cData)| orderId<int> | clientId<int> | product<chr> | gender<chr> | orderdate<chr> | Quantity<int> | Price<int> | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 255 | g | female | 3/1/2017 | 3 | 5 |
| 2 | 1 | 255 | a | female | 3/1/2017 | 3 | 14 |
| 3 | 1 | 255 | b | female | 3/1/2017 | 3 | 22 |
| 4 | 1 | 255 | a | female | 3/1/2017 | 1 | 14 |
| 5 | 2 | 145 | h | male | 5/1/2017 | 1 | 26 |
| 6 | 2 | 145 | h | male | 5/1/2017 | 1 | 26 |
6 rows
#Utilizamos la funcion summary() para ver qué datos tenemos
summary(cData)## orderId clientId product gender
## Min. : 1.0 Min. : 1.0 Length:4805 Length:4805
## 1st Qu.: 261.0 1st Qu.: 72.0 Class :character Class :character
## Median : 510.0 Median :143.0 Mode :character Mode :character
## Mean : 504.6 Mean :148.7
## 3rd Qu.: 750.0 3rd Qu.:224.0
## Max. :1000.0 Max. :300.0
## orderdate Quantity Price
## Length:4805 Min. :1.000 Min. : 5.0
## Class :character 1st Qu.:1.000 1st Qu.:12.0
## Mode :character Median :2.000 Median :14.0
## Mean :1.977 Mean :18.2
## 3rd Qu.:3.000 3rd Qu.:26.0
## Max. :3.000 Max. :32.0#comenzamos a explorar los datos
#install.packages("ggplot2")
library(ggplot2)
#install.packages("scales")
library(scales)Los graficos nos permiten llevar a lo visual la representación de los valores
#Graficamos la densidad en las transacciones
densidad=ggplot2::ggplot(cData)+ggplot2::geom_density(ggplot2::aes(x=Quantity*Price))+ggplot2::scale_x_continuous(labels=dollar)
plot(densidad)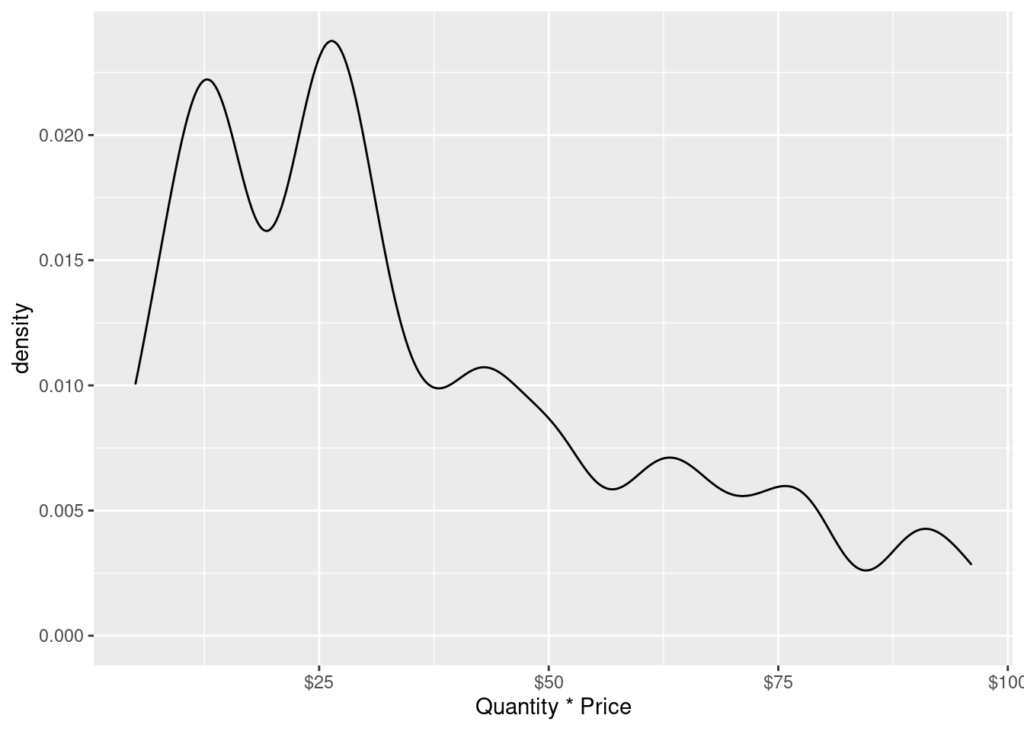
Esta grafica nos permite observar aquí que la mayoría de las tranasacciones rondan los 26 euros y en segundo lugar rondan los 12 euros, el resto cae rápidamente aportando menor relevancia.
#Visualizando los Datos en un histograma
histograma=ggplot2::ggplot(cData)+ggplot2::geom_histogram(ggplot2::aes(x=Quantity*Price), binwidth = 5, fill="gray")
plot(histograma)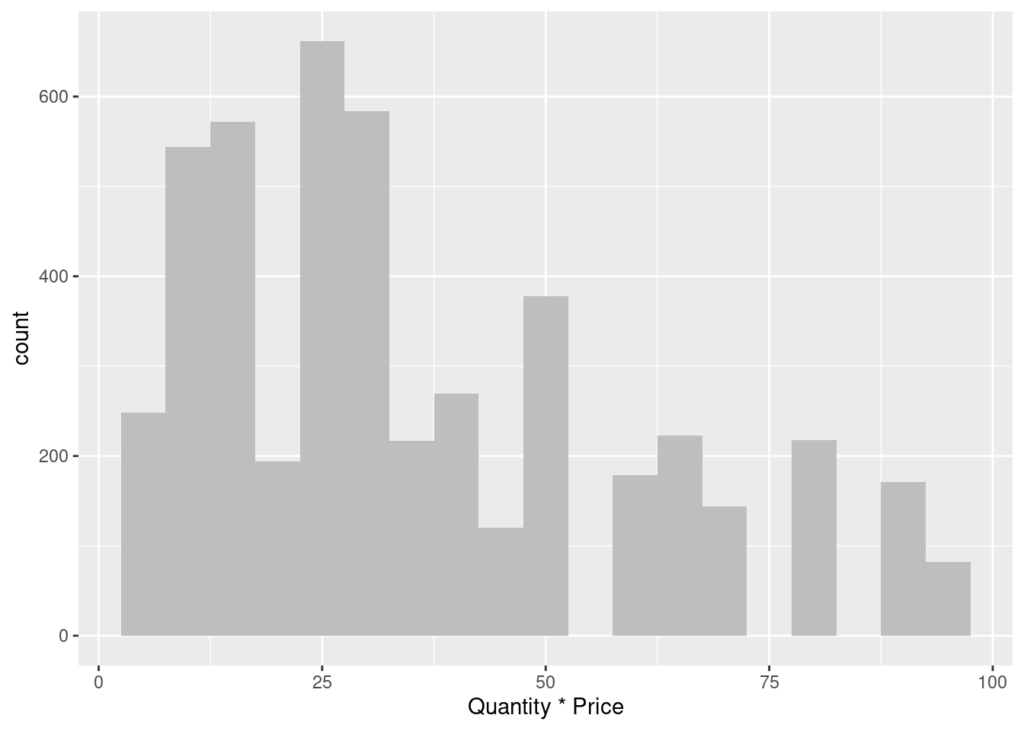
En el histograma se confirma, los valores picos en los 12 y 26 euros.
#La evolucion de las transacciones
plot(x = as.factor(cData$orderdate))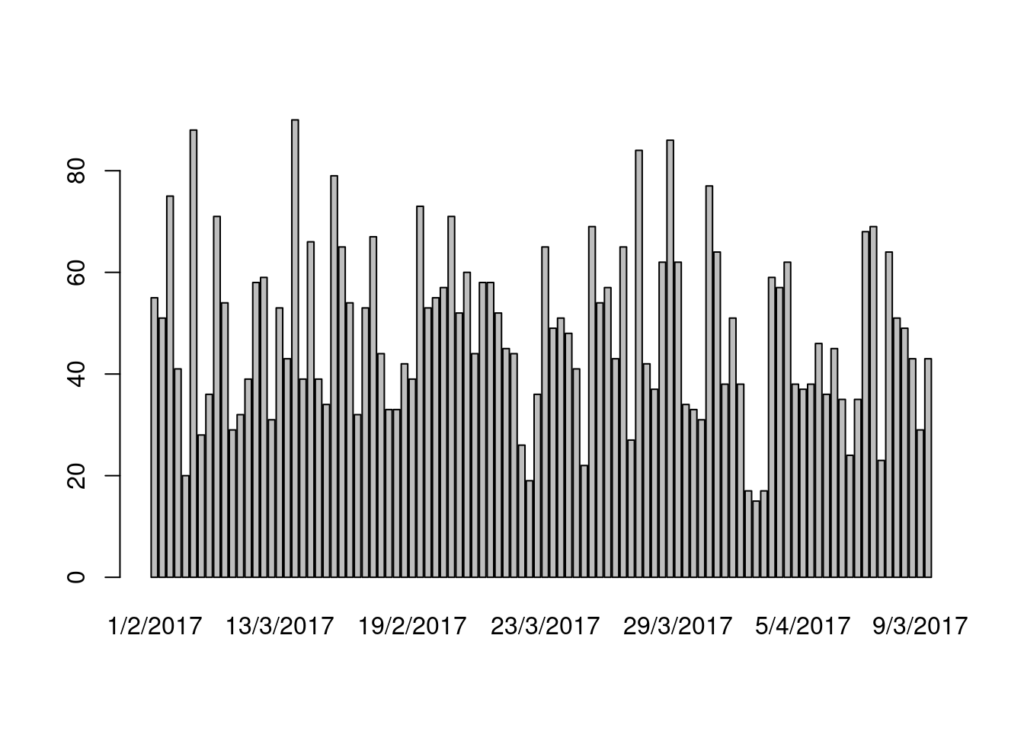
Aqui vemos la serie temporal de las transacciones y como se repiten.
#Miramos cuántas veces han comprado cada producto, para ver los más comprados
mascomprados<-ggplot2::ggplot(cData)+ggplot2::geom_bar(ggplot2::aes(x=product), fill="gray")+ggplot2::coord_flip()+ggplot2::theme(axis.text.y=ggplot2::element_text(size=ggplot2::rel(0.8)))
plot(mascomprados)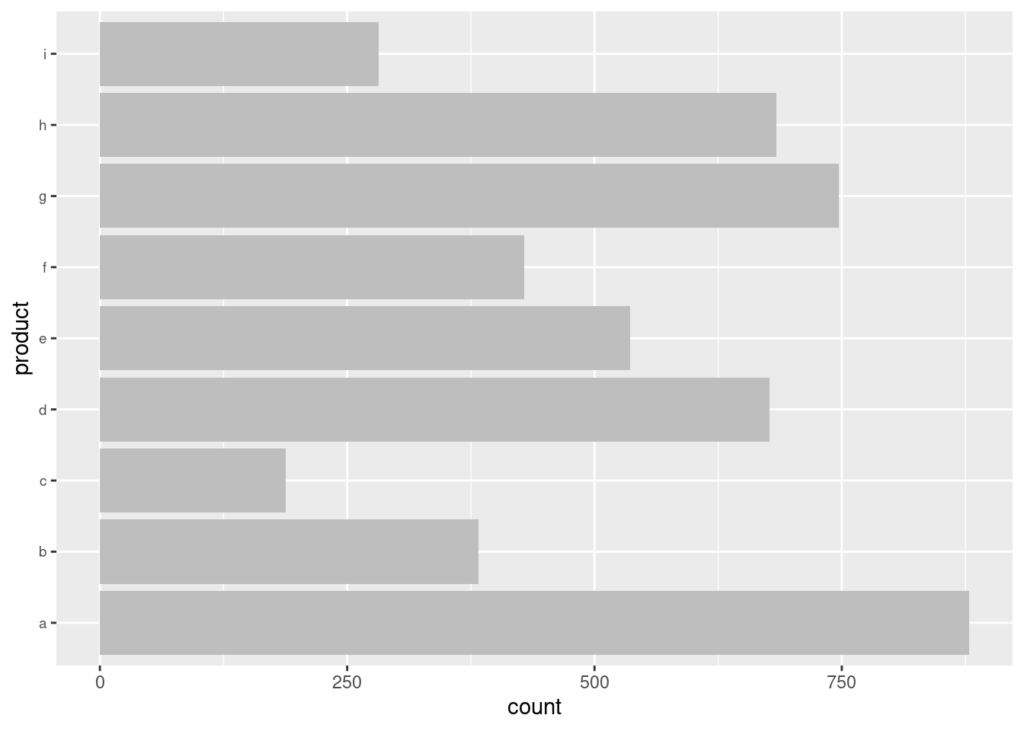
Ahora observamos cuáles han sido lo productos más comprados, y vemos que es primero el “a”, luego el “g” y tercero el “h”.
#Luego analizamos si alguno de los géneros coma más un producto
genderprod<-ggplot2::ggplot(cData)+ggplot2::geom_bar(ggplot2::aes(x=product, fill=gender),position = "dodge")
plot(genderprod)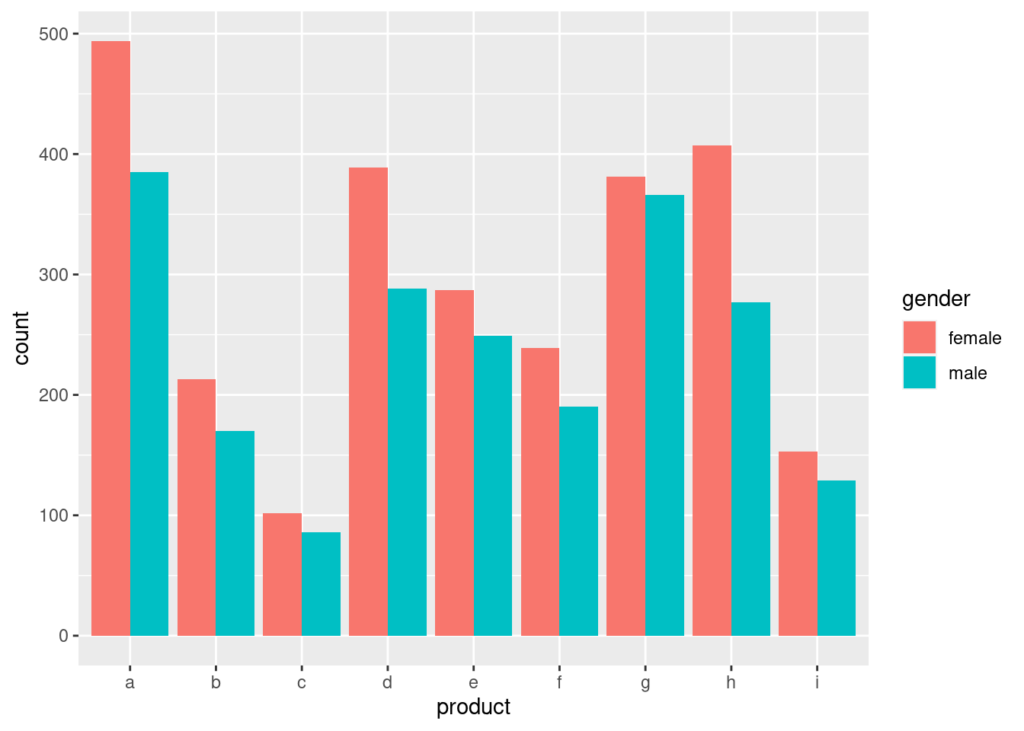
Finalmente vemos cómo son comprados los productos en cantidad según los géneros.
4) Análisis de agrupaciones:
El clustering es una manera de ordenar los datos en grupos en que los miembros del mismo grupo son más similares (Homogéneos)entre ellos que los que no son miembros del grupo, es decir que los grupos entre sí ssean lo más diferentes posible. Proyectaremos un clustering Jerarquico:
#DENDOGRAMA
Orders<-read.table("/cloud/project/Clustering/TransactionsCasoPractico.csv", header=TRUE, sep = ";")
head(Orders)| orderId<int> | clientId<int> | product<chr> | gender<chr> | orderdate<chr> | Quantity<int> | Price<int> | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 255 | g | female | 3/1/2017 | 3 | 5 |
| 2 | 1 | 255 | a | female | 3/1/2017 | 3 | 14 |
| 3 | 1 | 255 | b | female | 3/1/2017 | 3 | 22 |
| 4 | 1 | 255 | a | female | 3/1/2017 | 1 | 14 |
| 5 | 2 | 145 | h | male | 5/1/2017 | 1 | 26 |
| 6 | 2 | 145 | h | male | 5/1/2017 | 1 | 26 |
6 rows
GastoTotal<-aggregate.data.frame(Orders$Price*Orders$Quantity, by= list(Orders$product),sum)
colnames(GastoTotal)<-c("Producto","GastoTotal")
GastoTotal| Producto<chr> | GastoTotal<int> |
|---|---|
| a | 23982 |
| b | 16566 |
| c | 3420 |
| d | 15984 |
| e | 31710 |
| f | 20856 |
| g | 7520 |
| h | 34996 |
| i | 17408 |
9 rows
Para poder hacer clusters se necesitan nociones de similitud y disimilitud. La disimilitud se puede entender como la distancia en que los puntos de un cluster estén más cerca uno de otro que de los puntos de otros grupos. Analicemos la más popular, la Euclidiana:
#Calculamos la distancia
d<-dist(GastoTotal$GastoTotal, method = "euclidean")
#Cuya matriz resulta:
d## 1 2 3 4 5 6 7 8
## 2 7416
## 3 20562 13146
## 4 7998 582 12564
## 5 7728 15144 28290 15726
## 6 3126 4290 17436 4872 10854
## 7 16462 9046 4100 8464 24190 13336
## 8 11014 18430 31576 19012 3286 14140 27476
## 9 6574 842 13988 1424 14302 3448 9888 17588Ahora utilizamos la función hclust() que toma como input la matriz de distancias calculda (como a un objeto de clase dist) en que encontramos las distancias entre todas las parejas de puntos de los datos. Usamos también el método Ward, que empieza con cada punto como un cluster individual y va agrupando cluster iterativamente para minimizar el total de la suma de cuadrados del cluster resultante.
pfit<-hclust(d, method = "ward.D")
plot(pfit, labels=GastoTotal$Producto, main= " Dendograma de la tipología de productos por el gasto total de cada cliente", xlab= "Productos")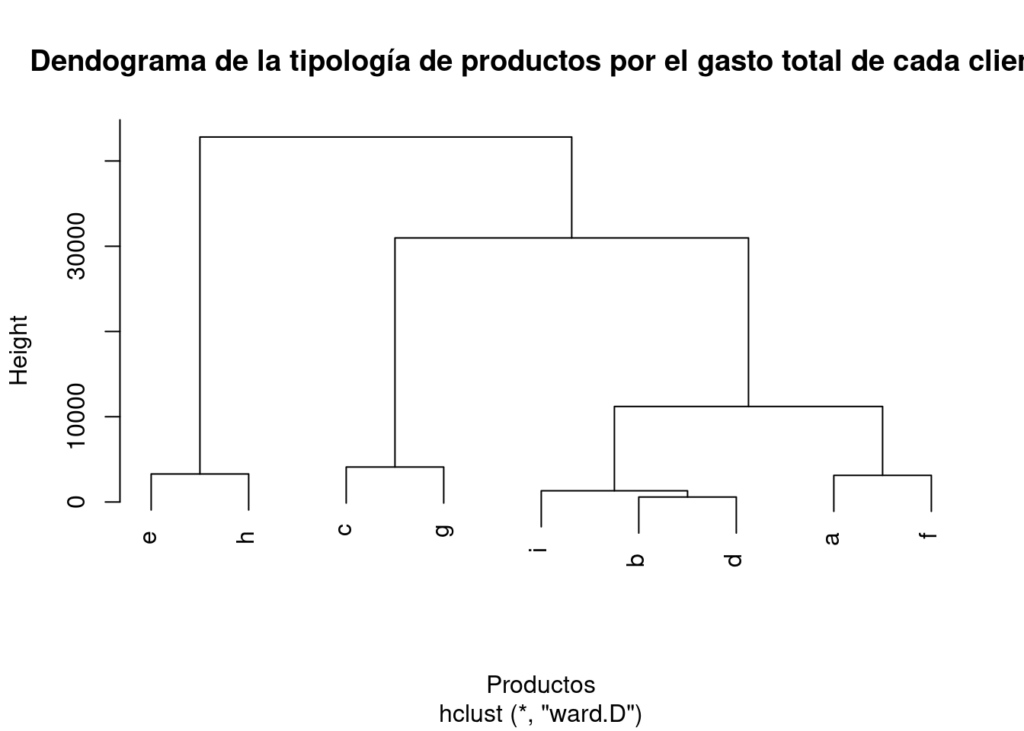
Como resultado el algoritmo nos sugiere 4 grupos, los que vamos a recuadrar:
#rect.hclust(pfit, k=4)También el ejercicio lo realicé en Rapidminer con los siguientes bloques:
Los resultados obtenidos en RM, varían por tener algunas parametrizaciones diferentes, pero lo importente con lo calculado es el concepto de observar que los 4 Clusters se construyeron también a partir de las similitud o cercanía en “distancias de gastos”:
